CS 115 Lab 6, Part B: Find the largest power of 2 less than a number

[Back to lab instructions]

The Big Picture

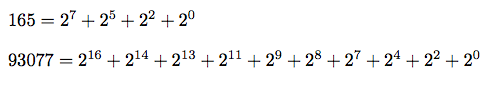
Any positive integer can be written as the sum of a series of terms, where each term is the number 2 raised to some power. For example:

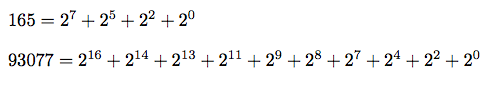
Note that in each of these two examples, the exponent of each term is less than that of its predecessor.

Over Parts B and C of this lab, you will write a program to read an integer and decompose it into such a series. Here is an example of how your final program might be used:

Enter a number: 1234
2**10 + 2**7 + 2**6 + 2**4 + 2**1

You will write this program in two steps. In the first step (Part B), your program reads an integer i_num, and finds the largest n such that
2ⁿ ≤ i_num. You can assume that the user always enters a positive integer.

Here is how this version of your program will interact with the user:

Enter a number: 1234
2**10

Note that 2¹⁰ is 1024, and 2¹¹ is 2048. The user's number, 1234, lies in between these two values. Therefore, 10 is the largest positive integer such that 2ⁿ ≤ i_num.

Here are a few more examples:

Enter a number: 165
2**7

Enter a number: 93077
2**16

Enter a number: 1
2**0

Instructions

Create a new Python source code file named lab06b.py:

"""
Program: CS 115 Lab 6b
Author: Your name
Description: This program will read a positive integer and
 find the largest power of two that is less than or equal to it.
"""


def main():
    # Read user's input and store it in a variable called i_num.
    # Initialize a variable n to serve as the exponent.
    # Initialize a variable two_to_n to hold the value of 2**n

    # while two_to_n is less than i_num:
        # add 1 to n
        # multiply two_to_n by 2
    
    # if two_to_n is greater than i_num:
        # subtract 1 from n
        # divide two_to_n by 2

    # Print the result


main()

Read the algorithm carefully, and decide on an appropriate initial value for n. This will also determine the initial value of two_to_n.

Before you fill in the code, answer Question 3 in your writeup. This question asks you to trace the values of n and two_to_n as this program processes the input 17. You should do this with pen and paper before filling in the code.

Once you understand the algorithm, replace the blue pseudocode with Python code.

Test your program. Here are some sample input/output sequences:

Sample 1

Enter a number: 1
2**0

Sample 2

Enter a number: 67
2**6

Sample 3

Enter a number: 127
2**6

Sample 4

Enter a number: 128
2**7

Sample 5

Enter a number: 129
2**7

When your program matches all of these examples, continue to Part C.